Hash – The Puzzle of Bitcoin (What Are the Miner's Mining?)

In the previous post we have explained the ideas behind the Bitcoin system, however, one issue remained unexplained: What is this bloody hard puzzle that the Bitcoin miners constantly try to solve?

Recall that in the Bitcoin system the miners are in constant competition: Whoever solves the puzzle first will earn the honor of adding a new block to the block-chain and make some money as well. Hence, the miners try feverishly to be the first to solve the puzzle. In the following section we are going to address the following questions:

• What exactly is this puzzle?
• How is it integrated in the Bitcoin system?

The Puzzle - A Cryptographic Hash Puzzle

Don’t be scared of the word ‘cryptography’, in our context it simply means that the ‘hash’ puzzle is related to the world of cryptography, i.e. building unbreakable systems.

Maybe the best real world analogy to a hash puzzle is a fingerprint.

Imagine that you are given a fingerprint sample and you are asked to discover the height, weight and overall look of the person to whom this fingerprint belongs. What would you do?

To make it a bit harder, assume that there is no correlation between fingerprints and other human features (like hair color) so the only way to test if this fingerprint came from your best friend is to take his fingerprint and compare it with the other one.

Thus, the most ideal approach would involve capturing fingerprints from every human being across the globe and sequentially matching them with the fingerprint under investigation until a match is identified and the process is halted. However, if luck is not on your side, you might end up identifying the correct person last. This means you would potentially continue this search for approximately 13,555 years, presuming you scrutinize one person per minute (given that the global population is around 7.125 billion individuals). On a more positive note, if fortune favors you, the expected duration to find the person would be halved - a minor victory, though the prospect might still appear daunting.

Let’s go back to our hash puzzle. In a hash puzzle, the fingerprint that you are given is a list of characters (let’s call it a word), like “dog”, after which your task is to find the right person (in our case this is a word as well) that produced the fingerprint. To this end the only thing you can do is to try all possible combinations of digits (of some length), one by one.

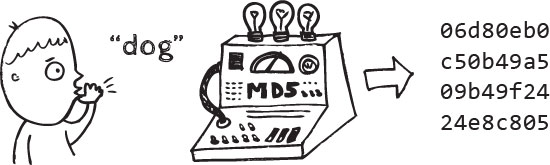
(Image source: https://blog.varonis.com/the-definitive-guide-to-cryptographic-hash-functions-part-1/)

Conceptually speaking, you have a machine that whenever you put some digits in it, it produces an output of some other combination of digits. You know completely nothing about this machine and it works like magic - you don’t see any correlation between the characters that you put in and the characters that it produces. The only rule that you have observed is that no matter how many characters you put in the machine, the produced output always has the same length.

One little technicality: The characters that are used by the machine (both your input and its output) are only composed by the ten digits 0-9 and the six letters a-f. This means that every character of the input or output could be one out of 16 characters.

The puzzle is essentially a word (list of characters), call it A, which represents the machine’s output, in order to solve it your task is to find the the correct input (another word), call iti B, such that when you put B into the machine you will get A as an output.

Starting with a simple case, suppose that the machine produces outputs of a single character. This means that there are only 16 different possible outputs. As an example, assume you got the character ‘d’ (as the puzzle) and the machine works in such a way that every character that is inserted leads to a different outputted character. Thus, if you try all possible characters 0-9 and a-f you will find the match, i.e. the character that when inserted in the machine produces the character ‘d’ as an output. In particular a minimum of 16 comparisons is required in order to be completely sure that a match will be found.

Complicating this a bit further, consider the case in which the machine produces an output of 2 characters instead of a single one, as in the previous example. This means that there are 16X16=256 different possible outputs. So when given some puzzle, ‘4c’ for instance, then you will need to try all possible inputs of 2 characters (i.e. ‘00’, ‘01’ … ’fd’,’fe’,’ff’) in order to guarantee a success.

Note that increasing the machine’s output length by a single character increases the number of trials you need to make by one order of magnitude (in our example by a factor of 16!). Thus, an output of a single character leads to 16 trials, an output of 2 characters leads to 256 trials, an output of 3 characters leads to 4096 trials, and so on.

So, ‘what’s the big deal?’ one might ask. Computers are so fast these days, you can build a software that will compute all trials for you in seconds!

Well, you might have noticed that the number of trials is growing in an exponential way! This means that for an output of x characters you will have to make x16 trials! For an output of 40 characters you will need to make 1461501637330902918203684832716283019655932542976 trials!! This number is so enormous no modern computer can make this number of trials even if it works constantly till the collapse of the solar system.

If you are still not convinced that the hash puzzle is a hard one, you might want to try it and find the solution to the following puzzle: Find a list of characters that when you put it through the SHA1 machine you get an output of all zero characters (that is ‘000000…’). The machine is available at sha1-online.com. Good luck 😉

The Connection to Bitcoin

Recall (from the previous post) that in every short time (usually 10 minutes) a single ‘block’ is appended to the ‘block-chain’ by a single ‘miner’ (the winer of the round). That miner, who appends that block, is the first one who found a solution to the hash puzzle. In order to understand this puzzle we need to know how does a block looks like. Details follow.

Briefly, a block in the block-chain is some data structure containing:

1. A nonce, this is the nucleus of the solution, the part of the block that entitles the miner the transaction fee.
2. A reference to the previous block - this is required in order to be able to track the history of all transaction, each block refers its predecessor, this way one can go back in history till the first block (You can track the transactions history at blockchain.info)
3. A list of all transactions to be processed if this block is appended to the block-chain.

In the figure below you can see these 3 properties: the nonce (in the last yellowed row), the reference (‘previous block hash’), and the list of transactions in greyed rows (the highlighted right hand side of the figure is explained soon).

(image source: http://www.righto.com/2014/09/mining-bitcoin-with-pencil-and-paper.html)

As mentioned, the miners are looking for the correct nonce that would solve the puzzle. The hash puzzle described in the previous question was a specific list of characters that the machine has produced as an output, in order to solve it one needs to find an input that produces this specific output.

In the bitcoin system, however, the hash puzzle is somewhat easier: Instead of chasing after a specific output, the miner needs to find an input that produces an output from a big set of allowed outputs. That is, a puzzle could be a list of characters such that its first 16 characters are ‘0’ while there is no limitation on the rest of the characters, they could be anything. Although this makes the puzzle a lot easier, it is a time and energy consuming problem to solve. In the figure above, the miner performs many trials in order to solve the puzzle, the only field that is permitted to be changed in each trial is the nonce. In every trial, the miner combines the nonce that it just chose, the list of transaction that it wished to add to the block-chain and the reference to the previous block all together, it then input it to the SHA1 machine. If the output of the SHA1 machine begins with 16 ‘0’ characters then it solved the puzzle and won the game.

Hope you enjoyed reading, see you in the next post!

Editor's Note: Transparency is one of our core values at vpnMentor, so you should know we are in the same ownership group as ExpressVPN. However, this does not affect our review process.